MRCALink Analysis for Coevolution of Plants and Endophytes
This information is available as a PDF.
Problem
Suppose we have a set of DNA sequences for host species H and a set of DNA sequences for parasite species P. We would like to study the co-evolution between the host species and the parasite species. More precisely, TH and TP are phylogenetic trees reconstructed from the data sets H and P. The hypotheses are:
- Null hypothesis: Trees TH and TP are independent.
- Alternative hypothesis: Trees TH and TP are not independent.
Data
We used 25 grasses and endophytes for full trees. See Table 1 for a list of species. For phylogenetic analysis, sequences from endophyte tub2 and tef1 genes were aligned, then concatenated into a single, contiguous sequence for each endophyte. Likewise, plant chloroplast sequences including two intergenic regions (trnT to trnL, and trnL to trnF) and the trnL intron sequence were aligned individually and concatenated to give a dataset of approximately the same size for each host grass, and then appended to yield a combined sequence alignment of approximately 2200 bp.
| Included in: | |||||
|---|---|---|---|---|---|
| Grasses | Endophytes | T1 | T2 | T3 | T4 |
| Brachyelytrum erectum (root) | Epichloë brachyelytri (root) | + | + | + | + |
| Brachypodium sylvaticum | Epichloë sylvatica 200751 | + | - | + | - |
| Echinopogon ovatus | Neotyphodium aotearoae 829 | + | - | + | - |
| Calamagrositis villosa | Epichloë baconii 200745 | + | + | + | + |
| Agrostis tenuis | Epichloë baconii 200746 | + | + | + | + |
| Agrostis hiemalis | Epichloë amarillans 200744 | + | + | + | + |
| Sphenopholis obtusata | Epichloë amarillans 200743 | + | + | + | + |
| Koeleria cristata | Epichloë festucae 1157 | + | + | - | - |
| Lolium sp. P4074 | Neotyphodium sp. FaTG2 4074 | + | + | + | + |
| Lolium sp. P4078 | Neotyphodium sp. FaTG3 4078 | + | + | + | + |
| Lolium arundinaceum | Neotyphodium coenophialum 19 | + | + | + | + |
| Lolium multiflorum | Neotyphodium occultans 999 | + | + | + | + |
| Lolium edwardii | Neotyphodium typhinum 989 | - | - | - | - |
| Lolium perenne | Epichloë typhina 200736 | - | - | - | - |
| Lolium perenne | Neotyphodium lolii 135 | + | + | - | - |
| Festuca rubra | Epichloë festucae 90661 | + | + | + | + |
| Festuca longifolia | Epichloë festucae 28 | + | + | + | + |
| Holcus mollis | Epichloë sp. 9924 | + | + | + | + |
| Hordelymus europaeus | Neotyphodium sp. 362 | + | + | + | + |
| Bromus ramosus | Epichloë bromicola 201558 | + | + | + | + |
| Bromus erectus | Epichloë bromicola 200749 | + | + | + | + |
| Bromus purgans | Epichloë elymi 1081 | + | + | - | - |
| Hordeum brevisubulatum | Neotyphodium sp. 3635 | + | + | + | + |
| Elymus canadensis | Epichloë elymi 201551 | + | + | + | + |
| Glyceria striata | Epichloë glyceriae 200755 | + | + | + | + |
| Achnatherum inebrians | Neotyphodium gansuense 818 | + | + | + | + |
Table 1: Hosts and symbionts: All listed taxa, as well as trimmed taxon sets T1-T4, were assessed for probability of codivergence.
MRCALink Algorithm
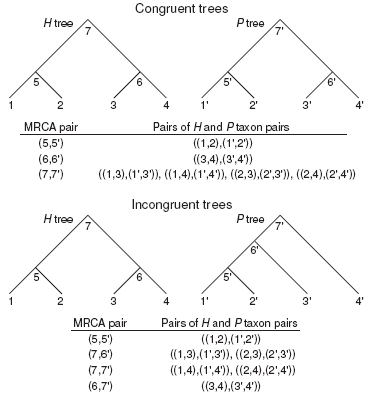
Figure 1: Simple examples of congruent and incongruent H and P trees, demonstrating the relationships of MRCA pairs to their corresponding pairs of H and P taxon pairs. In an ultrametric time tree, the distance between any two taxa is twice the age of their MRCA. In each tip clade a MRCA uniquely relates two taxa. However, a MRCA deeper in the tree relates multiple taxon pairs. Therefore, for congruent H and P trees the matrix of all pairwise distances of H taxon pairs against all pairwise distances of P taxon pairs represents each corresponding pair of tip clade MRCAs only once, and each corresponding pair of deeper MRCAs multiple times. This relationship is more complicated in the case of incongruent trees, which nevertheless tend to give greater representation to pairs of deeper MRCAs than to pairs of shallower MRCAs in pairwise distance matrices. The MRCALink algorithm samples corresponding H and P MRCA pairs only once.
The MRCALink algorithm introduced here identifies and stores each corresponding H and P MRCA pair. Crucially, the data for each corresponding MRCA pair is selected only once for subsequent statistical analysis. Trees must be strictly bifurcating for unique identification of valid pairs of H and P MRCAs. Note that the method does not assume an equal number of taxa in H and taxa in P, and also does not assume similar mutation rates in H and P. Given a set of host taxa H and a set of symbiont taxa P (“parasites,” in keeping with other literature in the field), there is a map called L : H → P such that a host A ∈ H has a parasite or symbiont L(A) ∈ P. Define MRCA(A,B) to be the node representing the Most Recent Common Ancestor (MRCA) of leaves A and B.
Algorithm 1 (The MRCALink Algorithm).
- Input a set of host taxa H, a set of parasite taxa P, a H tree TH, and a P tree TP where n1 is the number of taxa in H and n2 is the number of taxa in P.
- Output a set of MRCA pairs of host taxa and parasite taxa.
- Algorithm
Assign each node a unique number from 1 to 2n1 − 1 in the host tree and a unique number from 1 to 2n2 − 1 in the parasite tree such that a node i is ancestral to a node j.
Let U be a set of pairs of H and P node pairs, initially empty.
for (i from n1 + 1 to 2n1 − 1) do{
Set Xi = li × ri where li is the set of all left-descendents of i, and where ri is the set of all right-descendents of i.
/* This is just another way of saying Xi is all such pairs of one leaf from the left and one from the right. */
while (Xi ≠ ∅) do{
Choose x = MRCA(a, b) ∈ Xi and identify yj = MRCA(L(a),L(b)) for each distinct L(a) and L(b).
Remove x from Xi.
for (each distinct yj) do{
if (MRCA(x, yj) ∉ U) do{
U ← U ∪MRCA(x, yj).
}
}
}
}
Output U.
Dissimilarity method
We are interested in estimating the probability that the host and symbiont tree have some degree of dependence that may be due to a history of codivergence. To this end, we use the sets of all pairwise differences in H and P or the sets of pairwise differences in H and P from the the MRCA pairs sampled by the MRCALink algorithm. Let the sum of differences in uniquely estimated MRCA ages for trees A and B be S(A,B). The null hypothesis is that our TH and TP are independent, so we generate a distribution of S for pairs of unrelated random trees with the same number of leaves and root-to-tip normalized distances (i.e., we normalize the heights of TH and TP to 1) as TH and TP . Then we compare our S(TH, TP ) with this distribution. If the p-value is significantly low (< 0.05), we reject the null hypothesis and conclude that there is evidence of codivergence between TH and TP . To calculate S(A,B) with all pairwise distances, we take the sum of difference between pairwise distances for A and B over all pairwise distances. To calculate S(A,B) with the set of the MRCA pairs sampled by the MRCALink algorithm we take the sum of differences between pairwise distances for A and B over the set of the MRCA pairs sampled by the MRCALink algorithm.
We generate 10,000 random trees with the given branch lengths from the BDP via evolver from the PAML package for each TH and TP . For each tree, we used birth rate 0.5, death rate 0.5, and sampling fraction 1, 0.5, 0.001, 0.0005 (sampling fraction is the ratio of sample size to population size). We use the BDP for its biological justifications. Results are expressed as p, the probability that the pattern of corresponding node ages are independently developed. Thus, we reject the null hypothesis that TH and TP are independent if p is less than 0.05.
Results
Table 2: The p-values obtained by applying the dissimilarity method to all pairwise distances (noted by ALL) and to the MRCALink-derived matrix (noted by MRCA) for full and T1 – T4 plant and endophyte data sets (see Table 1 for the data sets). SF means a sampling fraction.
| Method | Data | SF = 0.0005 | SF = 0.001 | SF = 0.5 | SF = 1.0 |
|---|---|---|---|---|---|
| ALL | Full | 0.7843 | 0.7831 | 0.6768 | 0.3741 |
| MRCA | Full | 0.1234 | 0.1228 | 0.0813 | 0.0388 |
| ALL | T1 | 0.1165 | 0.115 | 0.0345 | 0.0089 |
| MRCA | T1 | < 0.001 | < 0.001 | < 0.001 | < 0.001 |
| ALL | T2 | 0.0934 | 0.0849 | 0.027 | 0.0116 |
| MRCA | T2 | < 0.001 | < 0.001 | < 0.001 | < 0.001 |
| ALL | T3 | 0.0639 | 0.0607 | 0.0173 | 0.0054 |
| MRCA | T3 | < 0.001 | < 0.001 | < 0.001 | < 0.001 |
| ALL | T4 | 0.0178 | 0.0199 | 0.0046 | 0.0017 |
| MRCA | T4 | < 0.001 | < 0.001 | < 0.001 | < 0.001 |
Table 3: The p-values obtained using the dissimilarity method with sub-optimal trees with 26 full and T1 – T4 plant and endophyte data sets (all taxa listed in Table 1) via the Bayesian MCMC method. ALL means the dissimilarity method with all pairwise distances and MRCA means the dissimilarity method with the MRCALink-derived matrix. SF means a sampling fraction. Each sampled tree is assigned number from 1 to 3 to distinguish it from the others.
| Method | Data | sample number | SF = 0.0005 | SF = 0.001 | SF = 0.5 | SF = 1.0 |
|---|---|---|---|---|---|---|
| ALL | Full | sample 1 | 0.7002 | 0.6858 | 0.4656 | 0.2942 |
| MRCA | Full | sample 1 | 0.0107 | 0.0112 | 0.0029 | 0.0018 |
| ALL | Full | sample 2 | 0.4742 | 0.4833 | 0.2452 | 0.1192 |
| MRCA | Full | sample 2 | 0.0636 | 0.0643 | 0.0253 | 0.0136 |
| ALL | Full | sample 3 | 0.6842 | 0.6833 | 0.4499 | 0.2617 |
| MRCA | Full | sample 3 | 0.193 | 0.1898 | 0.1022 | 0.0608 |
| ALL | T1 | sample 1 | 0.4505 | 0.4478 | 0.2361 | 0.1152 |
| MRCA | T1 | sample 1 | < 0.001 | < 0.001 | < 0.001 | < 0.001 |
| ALL | T1 | sample 2 | 0.0285 | 0.0327 | 0.0049 | 0.0009 |
| MRCA | T1 | sample 2 | < 0.001 | < 0.001 | < 0.001 | < 0.001 |
| ALL | T1 | sample 3 | 0.0064 | 0.007 | 0.0006 | < 0.001 |
| MRCA | T1 | sample 3 | < 0.001 | < 0.001 | < 0.001 | < 0.001 |
| ALL | T2 | sample 1 | 0.3459 | 0.3548 | 0.190 | 0.0965 |
| MRCA | T2 | sample 1 | < 0.001 | < 0.001 | < 0.001 | < 0.001 |
| ALL | T2 | sample 2 | 0.3547 | 0.3601 | 0.1836 | 0.0991 |
| MRCA | T2 | sample 2 | 0.0007 | 0.0001 | 0.0002 | < 0.001 |
| ALL | T2 | sample 3 | 0.0837 | 0.0788 | 0.0218 | 0.0103 |
| MRCA | T2 | sample 3 | < 0.001 | < 0.001 | < 0.001 | < 0.001 |
| ALL | T3 | sample 1 | 0.0695 | 0.0673 | 0.0202 | 0.0072 |
| MRCA | T3 | sample 1 | < 0.001 | < 0.001 | < 0.001 | < 0.001 |
| ALL | T3 | sample 2 | 0.0301 | 0.0293 | 0.0065 | 0.0297 |
| MRCA | T3 | sample 2 | < 0.001 | < 0.001 | < 0.001 | < 0.001 |
| ALL | T3 | sample 3 | 0.1318 | 0.1378 | 0.0498 | 0.0208 |
| MRCA | T3 | sample 3 | < 0.001 | < 0.001 | < 0.001 | < 0.001 |
| ALL | T4 | sample 1 | 0.1062 | 0.1029 | 0.0389 | 0.0147 |
| MRCA | T4 | sample 1 | < 0.001 | < 0.001 | < 0.001 | < 0.001 |
| ALL | T4 | sample 2 | 0.02407 | 0.0261 | 0.0069 | 0.0017 |
| MRCA | T4 | sample 2 | < 0.001 | < 0.001 | < 0.001 | < 0.001 |
| ALL | T4 | sample 3 | 0.0174 | 0.0161 | 0.0056 | 0.0015 |
| MRCA | T4 | sample 3 | < 0.001 | < 0.001 | < 0.001 | < 0.001 |
Software
- The algorithm to sampling pairs of MRCAs
only once and data sets. New Version as of August 15th
2013 MRCALink_new.tar.gz
the algorithm to sampling pairs of MRCAs only once and data sets. - the simulations for the numbers sampled at each pair of MRCAs. sampleTest.tar.gz
- The results via the dissimilarity methods. results.tar.gz.

